ロバスト推定法
-
※ロバスト推定を含めたフリーライブラリがあります ⇒ 詳しくはこちらへ
※ロバスト推定を簡単に試せるソフトウェアがあります ⇒ 詳しくはこちらへロバスト推定法とは
統計学の分野でロバスト推定法という考え方があり、誤差があるデータに対してその誤差の影響を最小にすることを目的とした理論です。ロバストとは「強靭さ」、「頑健さ」と訳される通り、外乱が発生してもそれに影響を受けにくく欠陥やエラーが生じないことを示す言葉で、ロバスト推定法という考え方はロバストとなるように物事を推定しようとの発想で生まれたものです。
画像処理への応用
画像処理は照明変動や対象ワークの表面状態等の多数の変動要因があり、それが誤差となって画像処理の邪魔をします。その誤差の発生の仕方を特定のモデルで推定し、安定した画像処理結果を得ることが出来るようにロバスト推定法が用いられます。誤差を含めたデータ解析の方法としては最小2乗推定法がありますが、この方法は個々のデータが均一の影響を持つものとして扱い、その誤差は正規分布とみなすことによって少数の特殊なデータに大きく影響を受けます。直線状に並んだ点の集合から直線を算出することを考えると、ノイズの影響で一点だけ大きく直線部分から外れた位置にある際にロバスト推定法は異常なデータの影響を排除することでより真実に近い直線を求めることを可能とします。
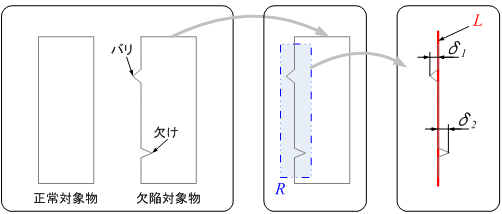
下図のような矩形形状をした対象物に発生する「バリ」や「欠け」を検出する場合を考えます。領域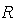 に対して対象物のエッジを抽出して直線
に対して対象物のエッジを抽出して直線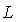 を求め、
を求め、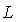 から各エッジまでの距離を算出することによりバリや欠けの最大高さである
から各エッジまでの距離を算出することによりバリや欠けの最大高さである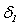 や
や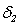 を算出します。予め与えられたしきい値とこれらを比較することで欠陥として検出ができます。
を算出します。予め与えられたしきい値とこれらを比較することで欠陥として検出ができます。
 これは下図(a)に示した直線
これは下図(a)に示した直線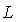 が算出されることを暗黙の前提としています。しかし、最小2乗推定法を用いて直線を求めると、欠けやバリに引っ張られて(b)に示した直線
が算出されることを暗黙の前提としています。しかし、最小2乗推定法を用いて直線を求めると、欠けやバリに引っ張られて(b)に示した直線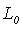 になってしまい、その結果、
になってしまい、その結果、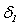 ・
・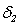 を正しく求めることができません。最小2乗推定法では全てのエッジを同じ重みで計算に使うので、これが問題となってきます。そこで、(c)に示した様に
を正しく求めることができません。最小2乗推定法では全てのエッジを同じ重みで計算に使うので、これが問題となってきます。そこで、(c)に示した様に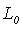 から離れたエッジほど直線算出の際に重みを下げた「重み付き最小2乗推定法」を使い、(d)に示した
から離れたエッジほど直線算出の際に重みを下げた「重み付き最小2乗推定法」を使い、(d)に示した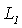 を求めます。
を求めます。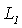 は
は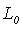 より
より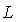 に近い直線になります。
に近い直線になります。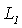 から再び各エッジの重みを求め、それを用いて直線を計算し直します。これらを何回も繰り返す事で直線が
から再び各エッジの重みを求め、それを用いて直線を計算し直します。これらを何回も繰り返す事で直線が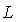 に近づいていきます。この手法を「ロバスト推定法」と言います。
に近づいていきます。この手法を「ロバスト推定法」と言います。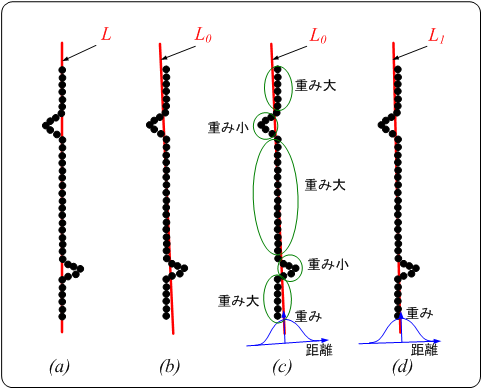
ロバスト推定法は直線算出だけでなく、最小2乗推定法で求められるもの、例えば円や楕円、アフィン変換、さらにはスカラ値といったものにも適用できます。下図に円およびアフィン変換の算出例を示します。
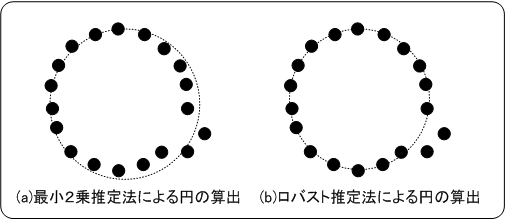
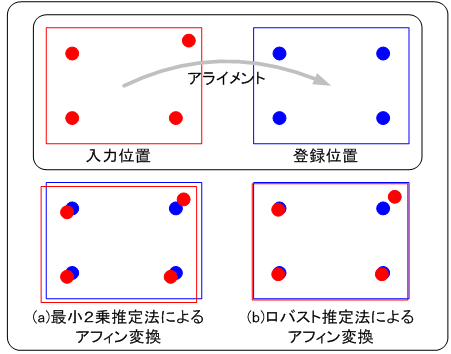
理論
ロバスト推定法は最小2乗推定法に重みの概念を組み込んだものですが、それに伴いもう1つ機能が必要になってきます。最小2乗推定法のように1回の計算で算出した場合は重みを計算の中に取り入れることができません。重みを調整しながら反復処理させ、より良い結果に収束させていくことで重みを上手に生かしています。重み付き反復最小2乗推定法がロバスト推定法の別名といっても良いでしょう。最小2乗推定法は(1)式に示した連立方程式を解いています。
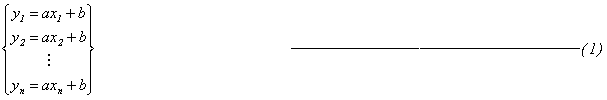
それに対して、ロバスト推定法は(1)式に重みを乗じた(2)式を連立させて解くことになります。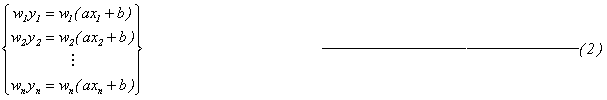 つまり、重み
つまり、重み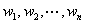 を更新しながら最小2乗推定法を反復して計算します。各点の重みを算出するのに(3)~(4)式に示した重み関数
を更新しながら最小2乗推定法を反復して計算します。各点の重みを算出するのに(3)~(4)式に示した重み関数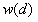 を導入します。この関数は、その時点までに推定した直線(下図の例では赤線)の位置を中心とした関数になります(重み関数はここで述べた以外にも種々のものが存在します)。
を導入します。この関数は、その時点までに推定した直線(下図の例では赤線)の位置を中心とした関数になります(重み関数はここで述べた以外にも種々のものが存在します)。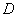 は外部より入力されるパラメータです。画像のS/Nにより
は外部より入力されるパラメータです。画像のS/Nにより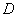 を制御します。もちろん、「S/N→大」なら「
を制御します。もちろん、「S/N→大」なら「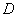 →小」です。理論上、
→小」です。理論上、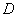 を無限大にすると最小2乗推定法と等価になります。
を無限大にすると最小2乗推定法と等価になります。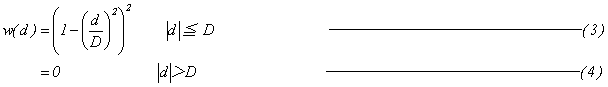
- 本例では点
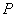 の重みは
の重みは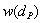 、点
、点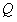 の重みは
の重みは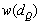 となります。
となります。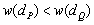 ですから、点
ですから、点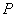 より点
より点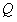 が高い寄与率を持つことになります。全ての点においてこの重みを算出し、それを使うことでロバスト推定法が実現できます。
が高い寄与率を持つことになります。全ての点においてこの重みを算出し、それを使うことでロバスト推定法が実現できます。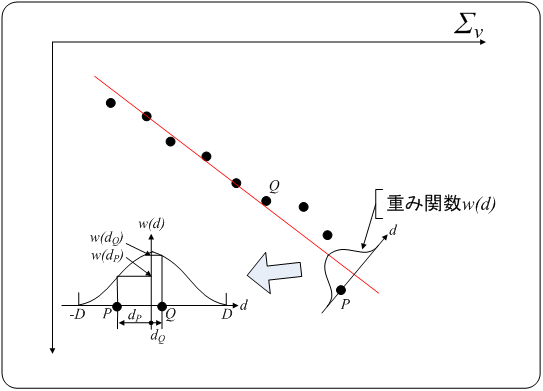 まず、
まず、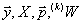 を次のように定義します。
を次のように定義します。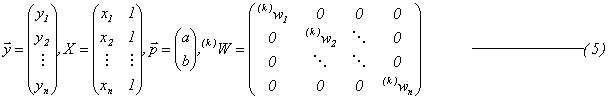
これにより、(2)式は(6)式のように表記されます。
(6)式を変形すると、
 となるので、
となるので、 の範囲で反復計算をすれば、
の範囲で反復計算をすれば、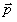 を求めることが出来ます。以下に(8)式を具体化した処理フローを示します。
を求めることが出来ます。以下に(8)式を具体化した処理フローを示します。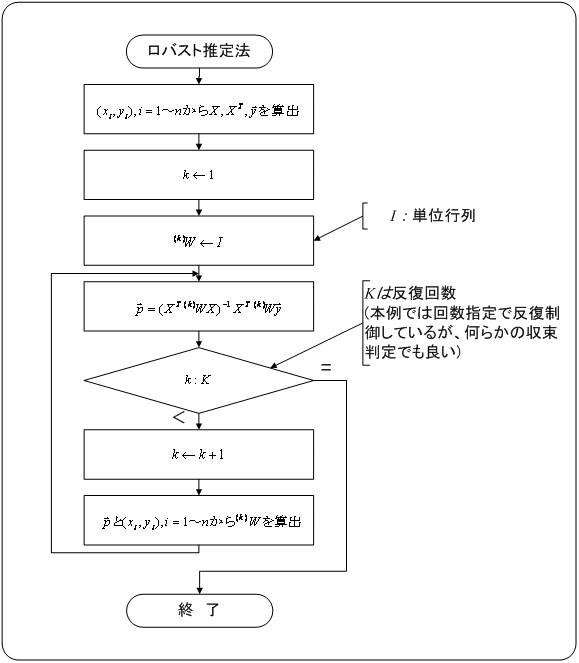
この処理により、下図の様に目的とする直線に徐々に収束していきます。
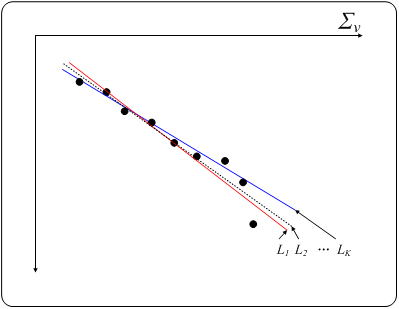 ここで、上図の記号の意味は以下の通りです。
ここで、上図の記号の意味は以下の通りです。
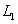 :通常の最小2乗推定法により推定された直線(全点の重みを1.0として計算)
:通常の最小2乗推定法により推定された直線(全点の重みを1.0として計算)
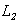 :各点毎の重みを考慮した重み付き最小2乗推定法により推定された直線
:各点毎の重みを考慮した重み付き最小2乗推定法により推定された直線
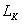 :重み付き最小2乗推定法を繰り返して最終的に推定された直線
:重み付き最小2乗推定法を繰り返して最終的に推定された直線※ロバスト推定を含めたフリーライブラリがあります ⇒ 詳しくはこちらへ
※ロバスト推定を簡単に試せるソフトウェアがあります ⇒ 詳しくはこちらへ
