ステレオ方式による３次元計測の理論 （第２版）

２眼ステレオ３次元計測ライブラリ

光切断３次元計測ライブラリ

キャリブレーションプレート

３次元画像処理とは

1台のカメラで画像を撮像して2次元の画像計測を行うことはごく普通のことですが、2台以上のカメラを使用して同じ場所を違った角度で撮像することによって撮像対象の3次元上の座標位置が2枚の画像から求められます。これは人の2つの眼が3次元空間を認識している方法である「両眼立体視」と基本的に同じもので、人は同じものを2つの眼で見ることによって生じる視差で瞬時に3次元空間上の位置を判断しています。人の目ではその位置を精度良く計測することはできませんが、カメラ間の位置関係が固定された撮像角度が異なる2台のカメラで同じ対象画像を捕捉し、コンピュータ処理することによって3次元座標を計測することができます。ただし、3次元座標の計測精度を高めるためには「事前にカメラ間の位置関係を精度良く求めておく」と「カメラで正確に対象画像を捕捉する」ことが大変重要となります。本技術説明では3次元座標の計測はどのような理論に基づいているのか、そして事前にカメラ間の位置関係を高精度で求めるため必須となるキャリブレーション理論について解説します。

実用化への取り組み

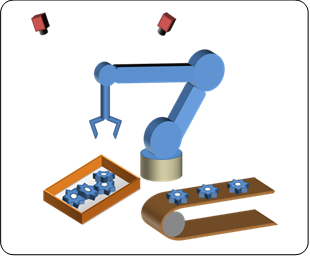
現在3D映画が話題を集めていますが、3次元の計測技術においてもファクトリーオートメーションの分野で大いに期待されています。ロボットハンドに2眼のカメラセットを搭載してばら積み部品をロボットでピッキングするピックアンドプレースへの応用、3次元空間内にある部品の組み立て用途、立体部品の形状計測や欠け・キズの検出等があります。これらのテーマは現状広く普及されていると言える段階ではありませんが、いろいろな企業で実用化への取り組みが盛んに進められています。

理論

3次元画像処理には、図0-1に示したように複数カメラを使ったものや光切断を使ったもの、あるいはそれらを組み合わせたもの等、種々の方法が存在します。ここでは一般的に用いられている2カメラを使った3次元画像処理の理論を説明します。

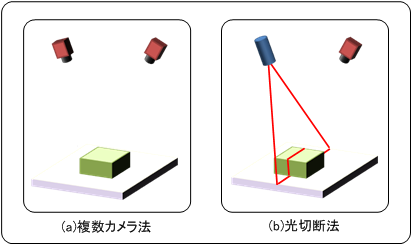
　　　　　　図0-1　３次元画像処理

アルゴリズムの説明に先だって、ここで使用する表記法を説明します。

◆ベクトルの表現法
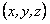座標をベクトル表現するのに以下の2つの方法を用いることにします。


これらはあくまでも表記が異なるだけで同値です。「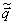」は「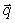の拡張ベクトル」と言います。なお、2次元の場合でも同様な表記法になります。

◆座標系および座標系上のベクトルの表現法
座標系は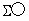で表します。装置の座標系によく使われるワールド座標系なら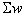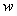（は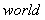の頭文字）となります。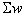上の座標を表す場合は、左上に座標系の名称を付して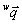のように記述します。さらに、座標に名前を付したいときは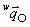といったように右下に記号を付けます。装置座標系上のマークを表す座標なら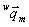といった記号で表わす事ができます。

◆行列の転置
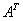は行列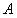の転置です。

ここから本題に入ります。3次元画像処理のアルゴリズムはかなり複雑になりますが、その処理の流れをまとめておきますと以下のようになります。

（１）対象物に割り付けた座標系とカメラに割り付けた座標系間の関係の導出

3次元画像処理は、複数のカメラで撮像した画像を使って対象物の3次元情報を抽出する処理です。それらを計算するためには、装置やカメラにそれぞれ座標系を割り付けて座標系の間の関係を導いておく必要があります。装置に割り付けた座標系を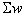、カメラに割り付けた座標系を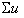とし、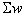上での3次元位置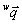に対してカメラで投影したものが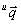となった場合、これらの関係は(0-3)式のような射影変換行列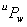を用いて表すことができます。


（２）射影変換行列の導出

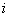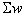全てのに対する上の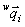が既知のキャリブレーション用基準治具があり、それら対応点が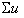上の対応点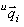として見出せるならば、 (0-3)式における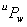を求めることができます。これは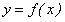がモデル式として与えられた場合、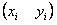のデータセットが適当な数だけ判るならば最小2乗法等により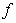が見出せるのと同じです（ただ、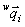と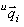の次元が異なるので最小2乗法よりは難しくなります）。先ほどの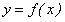の例における最小2乗法に相当するアルゴリズムが3次元画像処理でも幾つか存在します。その代表的なものに「Zhangの方法」と呼ばれるものがあります。なお、この項（２）の処理をカメラキャリブレーション（以下、「キャリブレーション」と略記）と言います。

（３）2つのカメラで得られた座標から3次元座標を導出

2つのカメラのキャリブレーションが終了していれば、



の2式における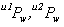が既に求まっている事になります。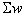内における同一の点を投影していることを保証された座標が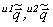として得られるならば、(0-4)式および(0-5)式を連立させて3次元座標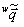を求めることができます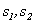（に関して言及しませんでしたが、これらは計算過程で消えて無くなります）。

上記の項（１）～項（３）に述べた内容は ステレオ方式による３次元計測の理論（第２版）に詳しく説明しています。